Kwave::Interpolation Class Reference

#include <Interpolation.h>

Collaboration diagram for Kwave::Interpolation:

Classes
class	InterpolationMap

Public Member Functions
	Interpolation (Kwave::interpolation_t type=INTPOL_LINEAR)
virtual	~Interpolation ()
bool	prepareInterpolation (const Kwave::Curve &points)
QVector< double >	interpolation (const Kwave::Curve &points, unsigned int len)
QVector< double >	limitedInterpolation (const Kwave::Curve &points, unsigned int len)
double	singleInterpolation (double pos)
double	singleLimitedInterpolation (double pos)
void	setType (Kwave::interpolation_t t)
Kwave::interpolation_t	type ()

Static Public Member Functions
static Kwave::interpolation_t	find (const QString &name)
static QString	name (Kwave::interpolation_t type)
static QStringList	descriptions (bool localized=false)
static Kwave::interpolation_t	findByIndex (int index)

Private Member Functions
unsigned int	count ()
void	createFullPolynom (const Kwave::Curve &points, QVector< double > &x, QVector< double > &y)
void	get2Derivate (const QVector< double > &x, const QVector< double > &y, QVector< double > &ab, unsigned int n)
void	createPolynom (const Kwave::Curve &points, QVector< double > &x, QVector< double > &y, int pos, unsigned int degree)

Private Attributes
const Kwave::Curve *	m_curve
QVector< double >	m_x
QVector< double >	m_y
QVector< double >	m_der
Kwave::interpolation_t	m_type

Static Private Attributes
static InterpolationMap	m_interpolation_map

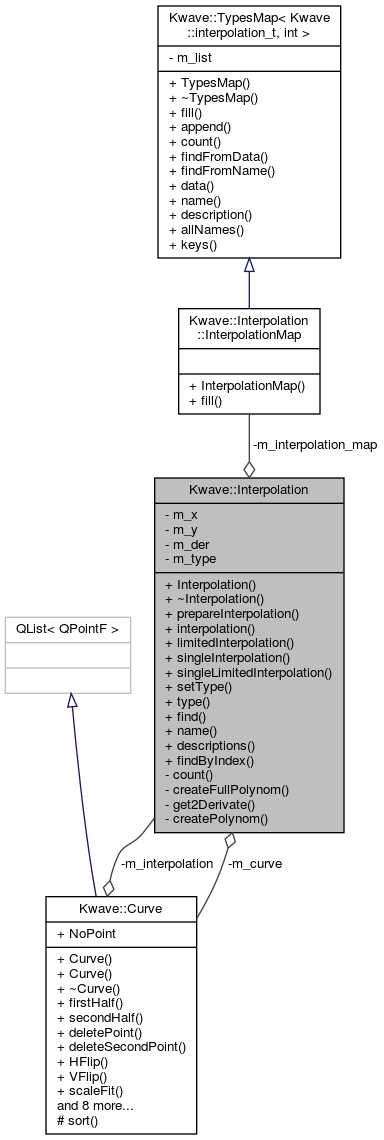
Detailed Description

Interpolation types

Definition at line 47 of file Interpolation.h.

Constructor & Destructor Documentation

Interpolation()

Kwave::Interpolation::Interpolation ( Kwave::interpolation_t  type = INTPOL_LINEAR )

explicit

Constructor, initializes type by enum type

Definition at line 51 of file Interpolation.cpp.

    :m_curve(), m_x(), m_y(), m_der(), m_type(type)
{
}

~Interpolation()

Kwave::Interpolation::~Interpolation ( )

virtual

Destructor.

Definition at line 57 of file Interpolation.cpp.

{
}

Member Function Documentation

count()

unsigned int Kwave::Interpolation::count ( )

private

Returns the number of points

Definition at line 81 of file Interpolation.cpp.

References m_curve.

Referenced by createFullPolynom(), createPolynom(), descriptions(), interpolation(), prepareInterpolation(), and singleInterpolation().

{
    return (m_curve ? m_curve->count() : 0);
}

Here is the caller graph for this function:

createFullPolynom()

void Kwave::Interpolation::createFullPolynom ( const Kwave::Curve &  points, QVector< double > &  x, QVector< double > &  y  )

private

???

Parameters

points	curve with points for interpolation
x	receives all x coordinates ???
y	receives all y coordinates ???

Definition at line 392 of file Interpolation.cpp.

References count(), and m_curve.

Referenced by interpolation(), and prepareInterpolation().

{
    Q_ASSERT(!points.isEmpty());
    Q_ASSERT(m_curve);
    if (points.isEmpty()) return;
    if (!m_curve) return;

    Q_ASSERT(points.count() == m_curve->count());
    if (points.count() != m_curve->count()) return;

    unsigned int count = 0;
    Kwave::Curve::ConstIterator it(points);
    while (it.hasNext()) {
        Kwave::Curve::Point p = it.next();
        x[count] = p.x();
        y[count] = p.y();
        count++;
    }

    for (unsigned int k = 0; k < count; k++)
        for (unsigned int j = k; j; ) {
            j--;
            y[j] = (y[j] - y[j+1]) / (x[j] - x[k]);
        }
}

Here is the call graph for this function:

Here is the caller graph for this function:

createPolynom()

void Kwave::Interpolation::createPolynom ( const Kwave::Curve &  points, QVector< double > &  x, QVector< double > &  y, int  pos, unsigned int  degree  )

private

???

Parameters

points	curve with points for interpolation
x	array of x coordinates
y	array of y coordinates
pos	???
degree	???

Definition at line 451 of file Interpolation.cpp.

References count().

Referenced by interpolation(), and singleInterpolation().

{
    unsigned int count = 0;
    Kwave::Curve::ConstIterator it(points);
    if (!it.hasNext()) return;
    Kwave::Curve::Point p = it.next();

    if (pos < 0) {
        switch (pos) {
           case -3:
                x[count] = -1.5;
                y[count++] = p.y();
                pos++;
                /* FALLTHROUGH */
           case -2:
                x[count] = -1.0;
                y[count++] = p.y();
                pos++;
                /* FALLTHROUGH */
            case -1:
                x[count] = -0.5;
                y[count++] = p.y();
                pos++;
                break;
        }
    }

    for (int i = 0; i < pos; i++)
        p = it.next();

    while ((count < degree) && it.hasNext()) {
        p = it.next();
        x[count]   = p.x();
        y[count++] = p.y();
    }

    int i = 1;
    it.toBack();
    p = it.previous();
    while (count < degree) {
        x[count]   = 1.0 + 0.5 * (i++);
        y[count++] = p.y();
    }

    // create coefficients in y[i] and x[i];
    for (unsigned int k = 0; k < degree; k++)
        for (int j = k - 1; j >= 0; j--)
            y[j] = (y[j] - y[j + 1]) / (x[j] - x[k]);

}

Here is the call graph for this function:

Here is the caller graph for this function:

descriptions()

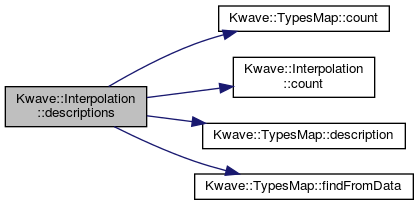
QStringList Kwave::Interpolation::descriptions ( bool  localized = false )

static

Returns an alphabetically sorted list of verbose interpolation type names, useful for providing a list of available types in the gui.

Parameters

localized

if true, the list will contain localized names (useful for filling combo boxes)

Definition at line 62 of file Interpolation.cpp.

References Kwave::TypesMap< IDX, DATA >::count(), count(), Kwave::TypesMap< IDX, DATA >::description(), Kwave::TypesMap< IDX, DATA >::findFromData(), and m_interpolation_map.

Referenced by Kwave::CurveWidget::CurveWidget().

{
    QStringList list;
    unsigned int count = m_interpolation_map.count();
    unsigned int i;
    for (i = 0; i < count; i++) {
        interpolation_t index = m_interpolation_map.findFromData(i);
        list.append(m_interpolation_map.description(index, localized));
    }
    return list;
}

Here is the call graph for this function:

Here is the caller graph for this function:

find()

static Kwave::interpolation_t Kwave::Interpolation::find ( const QString &  name )

inlinestatic

Returns the if of a type through it's name.

Parameters

name	the short name of the interpolation, like used in a command

Returns

the interpolation

Definition at line 83 of file Interpolation.h.

References name.

Referenced by Kwave::Curve::fromCommand().

        {
            return m_interpolation_map.findFromName(name);
        }

Here is the caller graph for this function:

findByIndex()

static Kwave::interpolation_t Kwave::Interpolation::findByIndex ( int  index )

inlinestatic

Translates an index in an interpolation type

Definition at line 114 of file Interpolation.h.

Referenced by Kwave::CurveWidget::selectInterpolationType().

                                                                  {
            return m_interpolation_map.findFromData(index);
        }

Here is the caller graph for this function:

get2Derivate()

void Kwave::Interpolation::get2Derivate ( const QVector< double > &  x, const QVector< double > &  y, QVector< double > &  ab, unsigned int  n  )

private

???

Parameters

x	array of x coordinates
y	array of y coordinates
ab	array for return values
n	???

Definition at line 420 of file Interpolation.cpp.

Referenced by interpolation(), and prepareInterpolation().

{
    Q_ASSERT(n);
    if (!n) return;

    unsigned int i, k;
    QVector<double> u(n);

    ab[0] = ab[1] = 0;
    u[0] = u[1] = 0;

    for (i = 2; i < n; ++i) {
        const double sig = (x[i] - x[i-1]) / (x[i+1] - x[i-1]);
        const double p   = sig * ab[i-1] + 2;
        ab[i] = (sig-1) / p;
        u[i] = (y[i+1] - y[i])   / (x[i+1] - x[i])
             - (y[i]   - y[i-1]) / (x[i]   - x[i-1]);
        u[i] = (6 * u[i] / (x[i+1] - x[i-1]) - sig * u[i-1]) / p;
    }

    const double qn = 0;
    const double un = 0;
    ab[n] = (un - qn * u[n - 1]) / (qn * ab[n - 1] + 1);

    for (k = n - 1; k > 0; --k)
        ab[k] = ab[k] * ab[k + 1] + u[k];

}

Here is the caller graph for this function:

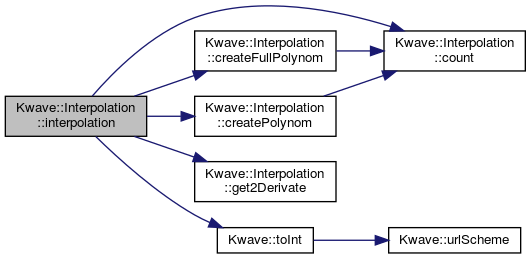
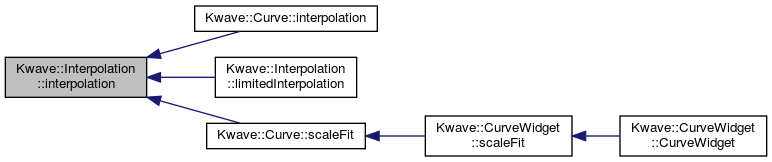
interpolation()

QVector< double > Kwave::Interpolation::interpolation	(	const Kwave::Curve &	points,
		unsigned int	len
	)

Definition at line 221 of file Interpolation.cpp.

References count(), createFullPolynom(), createPolynom(), get2Derivate(), Kwave::INTPOL_LINEAR, Kwave::INTPOL_NPOLYNOMIAL, Kwave::INTPOL_POLYNOMIAL3, Kwave::INTPOL_POLYNOMIAL5, Kwave::INTPOL_POLYNOMIAL7, Kwave::INTPOL_SAH, Kwave::INTPOL_SPLINE, m_type, and Kwave::toInt().

Referenced by Kwave::Curve::interpolation(), limitedInterpolation(), and Kwave::Curve::scaleFit().

{
    Q_ASSERT(len);
    if (!len) return QVector<double>();

    unsigned int degree = 0;
    QVector<double> y_out(len, 0.0);

    switch (m_type) {
        case INTPOL_LINEAR:
        {
            Kwave::Curve::ConstIterator it(points);

            if (it.hasNext()) {
                Kwave::Curve::Point p = it.next();
                double x0 = p.x();
                double y0 = p.y();

                while (it.hasNext()) {
                    p = it.next();
                    const double x1 = p.x();
                    const double y1 = p.y();

                    double dy = (y1 - y0);
                    int dx  = Kwave::toInt((x1 - x0) * len);
                    int min = Kwave::toInt(x0 * len);

                    Q_ASSERT(x0 >= 0.0);
                    Q_ASSERT(x1 <= 1.0);
                    for (int i = Kwave::toInt(x0 * len);
                         i < Kwave::toInt(x1 * len); i++) {
                        double h = dx ? ((double(i - min)) / dx) : 0.0;
                        y_out[i] = y0 + (h * dy);
                    }
                    x0 = x1;
                    y0 = y1;
                }
            }
            break;
        }
        case INTPOL_SPLINE:
        {
            int t = 1;
            unsigned int count = points.count();

            double ny = 0;
            QVector<double> der(count + 1);
            QVector<double> x(count + 1);
            QVector<double> y(count + 1);

            Kwave::Curve::ConstIterator it(points);
            while (it.hasNext()) {
                Kwave::Curve::Point p = it.next();
                x[t] = p.x();
                y[t] = p.y();
                t++;
            }

            get2Derivate(x, y, der, count);

            int start = Kwave::toInt(x[1] * len);

            for (unsigned int j = 2; j <= count; j++) {
                const int ent = Kwave::toInt(x[j] * len);
                for (int i = start; i < ent; i++) {
                    const double xin = static_cast<double>(i) / len;
                    const double h   = x[j] - x[j - 1];

                    if (!qFuzzyIsNull(h)) {
                        const double a = (x[j] - xin) / h;
                        const double b = (xin - x[j - 1]) / h;

                        ny = (a * y[j - 1] + b * y[j] +
                                ((a * a * a - a) * der[j - 1] +
                                (b * b * b - b) * der[j]) * (h * h) / 6.0);
                    }

                    y_out[i] = ny;
                    start = ent;
                }
            }
            break;
        }
        case INTPOL_POLYNOMIAL3:
            if (!degree) degree = 3;
            /* FALLTHROUGH */
        case INTPOL_POLYNOMIAL5:
            if (!degree) degree = 5;
            /* FALLTHROUGH */
        case INTPOL_POLYNOMIAL7:
        {
            if (!degree) degree = 7;
            const unsigned int count = points.count();
            QVector<double> x(7);
            QVector<double> y(7);

            if (count) {
                for (unsigned int px = 0; px < count - 1; px++) {
                    createPolynom (points, x, y, px - degree / 2, degree);
                    const double start = points[px].x();

                    double ent;
                    if (px >= count - degree / 2 + 1)
                        ent = 1;
                    else
                        ent = points[px + 1].x();

                    for (int i = Kwave::toInt(start * len);
                        i < Kwave::toInt(ent * len); i++)
                    {
                        double ny = y[0];
                        for (unsigned int j = 1; j < degree; j++)
                            ny = ny * ((static_cast<double>(i)) / len - x[j])
                                + y[j];

                        y_out[i] = ny;
                    }
                }
            }
            break;
        }
        case INTPOL_NPOLYNOMIAL:
        {
            const int count = points.count();
            if (count != 0) {
                QVector<double> x(count+1);
                QVector<double> y(count+1);

                createFullPolynom(points, x, y);

                for (unsigned int i = 1; i < len; i++) {
                    const double px = static_cast<double>(i) / len;
                    double ny = y[0];
                    for (int j = 1; j < count; j++)
                        ny = ny * (px - x[j]) + y[j];

                    y_out[i] = ny;
                }
            }
            break;
        }
        case INTPOL_SAH:
        {
            Kwave::Curve::ConstIterator it(points);
            if (it.hasNext()) {
                Kwave::Curve::Point p = it.next();
                double x0 = p.x();
                double y0 = p.y();

                while (it.hasNext()) {
                    p = it.next();
                    const double x1 = p.x();
                    const double y1 = p.y();

                    for (int i = Kwave::toInt(x0 * len);
                         i < Kwave::toInt(x1 * len); i++)
                        y_out[i] = y0;

                    x0 = x1;
                    y0 = y1;
                }
            }
            break;
        }
    }

    return y_out;
}

Here is the call graph for this function:

Here is the caller graph for this function:

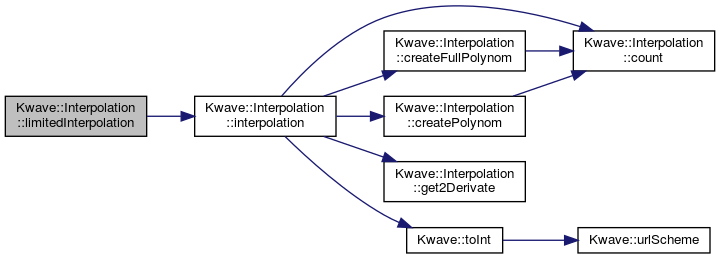
limitedInterpolation()

QVector< double > Kwave::Interpolation::limitedInterpolation	(	const Kwave::Curve &	points,
		unsigned int	len
	)

Definition at line 209 of file Interpolation.cpp.

References interpolation().

{
    QVector<double> y = interpolation(points, len);
    for (unsigned int i = 0; i < len; i++) {
        if (y[i] > 1) y[i] = 1;
        if (y[i] < 0) y[i] = 0;
    }
    return y;
}

Here is the call graph for this function:

name()

QString Kwave::Interpolation::name ( Kwave::interpolation_t  type )

static

Returns the name of an interpolation (non-localized).

Parameters

type	the type to get the name of

Definition at line 75 of file Interpolation.cpp.

References m_interpolation_map, and Kwave::TypesMap< IDX, DATA >::name().

Referenced by Kwave::Curve::getCommand().

{
    return m_interpolation_map.name(type);
}

Here is the call graph for this function:

Here is the caller graph for this function:

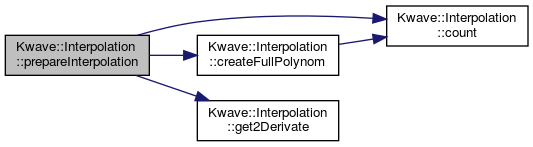
prepareInterpolation()

bool Kwave::Interpolation::prepareInterpolation

(

const Kwave::Curve &

points

)

Definition at line 175 of file Interpolation.cpp.

References count(), createFullPolynom(), get2Derivate(), Kwave::INTPOL_NPOLYNOMIAL, Kwave::INTPOL_SPLINE, m_curve, m_der, m_type, m_x, and m_y.

Referenced by Kwave::Curve::interpolation().

{
    m_curve = &points;
    if (!count()) return false; // no data ?

    m_x   = QVector<double>((count() + 1), double(0.0));
    m_y   = QVector<double>((count() + 1), double(0.0));
    m_der = QVector<double>();

    unsigned int c = 0;
    Kwave::Curve::ConstIterator it(points);
    while (it.hasNext()) {
        Kwave::Curve::Point p = it.next();
        m_x[c] = p.x();
        m_y[c] = p.y();
        c++;
    }
    m_x[c] = m_y[c] = 0.0;

    switch (m_type) {
        case INTPOL_NPOLYNOMIAL:
            createFullPolynom(points, m_x, m_y);
            break;
        case INTPOL_SPLINE:
            m_der = QVector<double>((count() + 1), double(0.0));
            get2Derivate(m_x, m_y, m_der, count());
            break;
        default:
            ;
    }
    return true;
}

Here is the call graph for this function:

Here is the caller graph for this function:

setType()

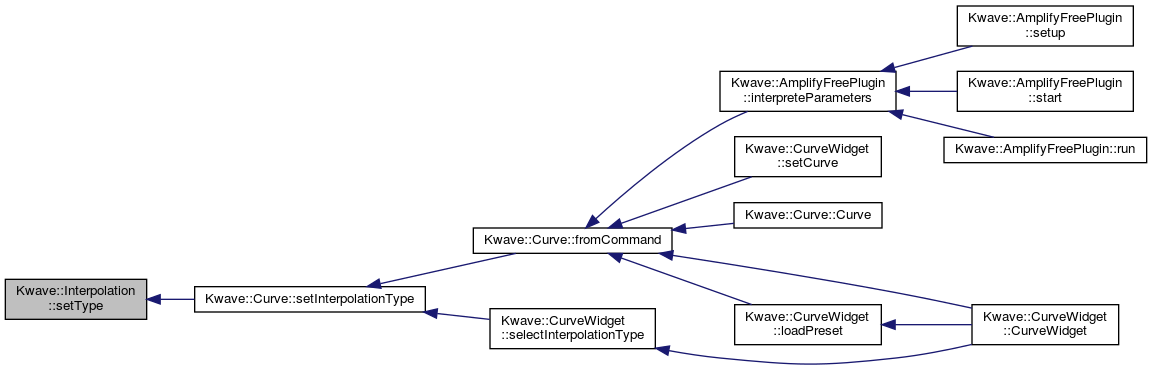
void Kwave::Interpolation::setType ( Kwave::interpolation_t  t )

inline

Sets a new interpolation tpye

Definition at line 104 of file Interpolation.h.

Referenced by Kwave::Curve::setInterpolationType().

                                                     {
            m_type = t;
        }

Here is the caller graph for this function:

singleInterpolation()

double Kwave::Interpolation::singleInterpolation

(

double

pos

)

Returns a single point of the interpolation.

=0 per definition

Definition at line 87 of file Interpolation.cpp.

References count(), createPolynom(), Kwave::INTPOL_LINEAR, Kwave::INTPOL_NPOLYNOMIAL, Kwave::INTPOL_POLYNOMIAL3, Kwave::INTPOL_POLYNOMIAL5, Kwave::INTPOL_POLYNOMIAL7, Kwave::INTPOL_SAH, Kwave::INTPOL_SPLINE, m_curve, m_der, m_type, m_x, and m_y.

Referenced by Kwave::CurveStreamAdapter::goOn().

{
    if (!count()) return 0.0; // no data ?

    unsigned int degree = 0;
    unsigned int count = this->count();

    if (input < 0.0) input = 0.0;
    if (input > 1.0) input = 1.0;

    switch (m_type) {
        case INTPOL_LINEAR:
            {
                unsigned int i = 1;
                while ((i < count) && (m_x[i] < input))
                    i++;

                double dif1 = m_x[i] - m_x[i-1];  
                double dif2 = input - m_x[i-1];

                return (m_y[i-1] + ((m_y[i] - m_y[i-1])*dif2 / dif1));
            }
        case INTPOL_SPLINE:
            {
                double a, b, diff;
                unsigned int j = 1;

                while ((j < count) && (m_x[j] < input))
                    j++;

                diff = m_x[j] - m_x[j-1];

                a = (m_x[j] - input) / diff;    //div should not be 0
                b = (input - m_x[j-1]) / diff;

                return (a*m_y[j-1] + b*m_y[j] + ((a*a*a - a)*m_der[j - 1] +
                       (b*b*b - b)*m_der[j])*(diff*diff) / 6);
            }
        case INTPOL_NPOLYNOMIAL:
            {
                double ny = m_y[0];
                for (unsigned int j = 1; j < count; j++)
                    ny = ny * (input - m_x[j]) + m_y[j];
                return ny;
            }
        case INTPOL_SAH:     //Sample and hold
            {
                unsigned int i = 1;
                while ((i < count) && (m_x[i] < input))
                    i++;
                return m_y[i-1];
            }
        case INTPOL_POLYNOMIAL3:
            degree = 3;
            break;
        case INTPOL_POLYNOMIAL5:
            degree = 5;
            break;
        case INTPOL_POLYNOMIAL7:
            degree = 7;
            break;
    }

    if (degree && (degree <= 7)) {
        Q_ASSERT(m_curve);
        if (!m_curve) return 0;

        // use polynom
        double ny;
        QVector<double> ax(7);
        QVector<double> ay(7);

        unsigned int i = 1;
        while ((i < count) && (m_x[i] < input))
            i++;

        createPolynom(*m_curve, ax, ay, i - 1 - degree/2, degree);

        ny = ay[0];
        for (unsigned int j = 1; j < degree; j++)
            ny = ny * (input - ax[j]) + ay[j];
        return ny;
    }

    return 0;
}

Here is the call graph for this function:

Here is the caller graph for this function:

singleLimitedInterpolation()

double Kwave::Interpolation::singleLimitedInterpolation

(

double

pos

)

Same as getSingleInterpolation, but return value will be limited to be [0...1]

See also

singleInterpolation

Parameters

pos

???

Returns

interpolated value [0...1]

type()

Kwave::interpolation_t Kwave::Interpolation::type ( )

inline

Returns the currently interpolation selected type

Definition at line 109 of file Interpolation.h.

Referenced by Kwave::Curve::getCommand(), Kwave::Curve::interpolationType(), and Kwave::Curve::scaleFit().

                                           {
            return m_type;
        }

Here is the caller graph for this function:

Member Data Documentation

m_curve

const Kwave::Curve* Kwave::Interpolation::m_curve

private

List of points to be interpolated.

Definition at line 181 of file Interpolation.h.

Referenced by count(), createFullPolynom(), prepareInterpolation(), and singleInterpolation().

m_der

QVector<double> Kwave::Interpolation::m_der

private

??? used for temporary purposes

Definition at line 190 of file Interpolation.h.

Referenced by prepareInterpolation(), and singleInterpolation().

m_interpolation_map

Kwave::Interpolation::InterpolationMap Kwave::Interpolation::m_interpolation_map

staticprivate

Map with type and name of interpolations

Definition at line 193 of file Interpolation.h.

Referenced by descriptions(), Kwave::Interpolation::InterpolationMap::fill(), and name().

m_type

Kwave::interpolation_t Kwave::Interpolation::m_type

private

Type of the interpolation.

Definition at line 196 of file Interpolation.h.

Referenced by interpolation(), prepareInterpolation(), and singleInterpolation().

m_x

QVector<double> Kwave::Interpolation::m_x

private

??? used for temporary purposes

Definition at line 184 of file Interpolation.h.

Referenced by prepareInterpolation(), and singleInterpolation().

m_y

QVector<double> Kwave::Interpolation::m_y

private

??? used for temporary purposes

Definition at line 187 of file Interpolation.h.

Referenced by prepareInterpolation(), and singleInterpolation().

---

The documentation for this class was generated from the following files:

• libkwave/Interpolation.h
• libkwave/Interpolation.cpp